注意:以下節目部份內容可能不適合正常人類觀看,敬請家長留意
上篇我們似乎找到了逃離Σ迷宮的出路,可是過程中有一個致命缺點:我們曾經“不管對錯”,假設了 In 滿足以下規律:
萬一這個規律不成立呢?我們豈非前功盡廢?
好!這一節我們就來道證明題,證明 In 滿足上述規律。
我們已經證明了,對於 n =1 ~ 4,上式都是成立的。現在採取這樣的辨法:
假設等式
對於 k =1 ~ (n-1) 都成立,求證 k = n 時等式也成立。
我們在第一節走了不少冤枉路,但也絕非一無所獲。還記得以下內容嗎?
規律開始出來了,對於第 n 期,其“本金”就是 t - (x - I1) - (x - I2) - ... - (x - In-1),對應的利息 In 則為:
其中
即
接下來神奇的事情要發生了!我們知道,式中的 (1+p) 是一個常數,我們不妨將它記為 α,即:
於是 In 變為:
式子很長很長(請點開放大),但是,注意看,大部份的 α 都已經互相抵消掉了,只剩頭尾兩項!即:
現在再把 α = 1 + p 代入式中,有:
你或許還未注意到,不知不覺間,命題已經證畢了。等式成立了:
~~~~~~~~~~~~~~第三節完~~~~~~~~~~~~~~







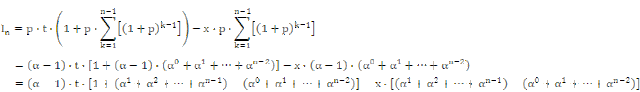



沒有留言:
張貼留言