【超簡單】用尺規法畫一條線段的n等分點

因為不記得尺規作圖能不能用三角板了（主要作用是畫平行線），以下便假設不能用，並以五等分點為例，介紹如何簡單地畫一條線段的n等分點（n為任意正整數）。

【題目】已知一線段AB（如圖），用尺規法找出它的五等分點。

【解】

註：以下圖中，黑色為題設條件，綠色為直尺作圖痕跡，紅色為圓規作圓痕跡，橙色為標注，藍色為答案。

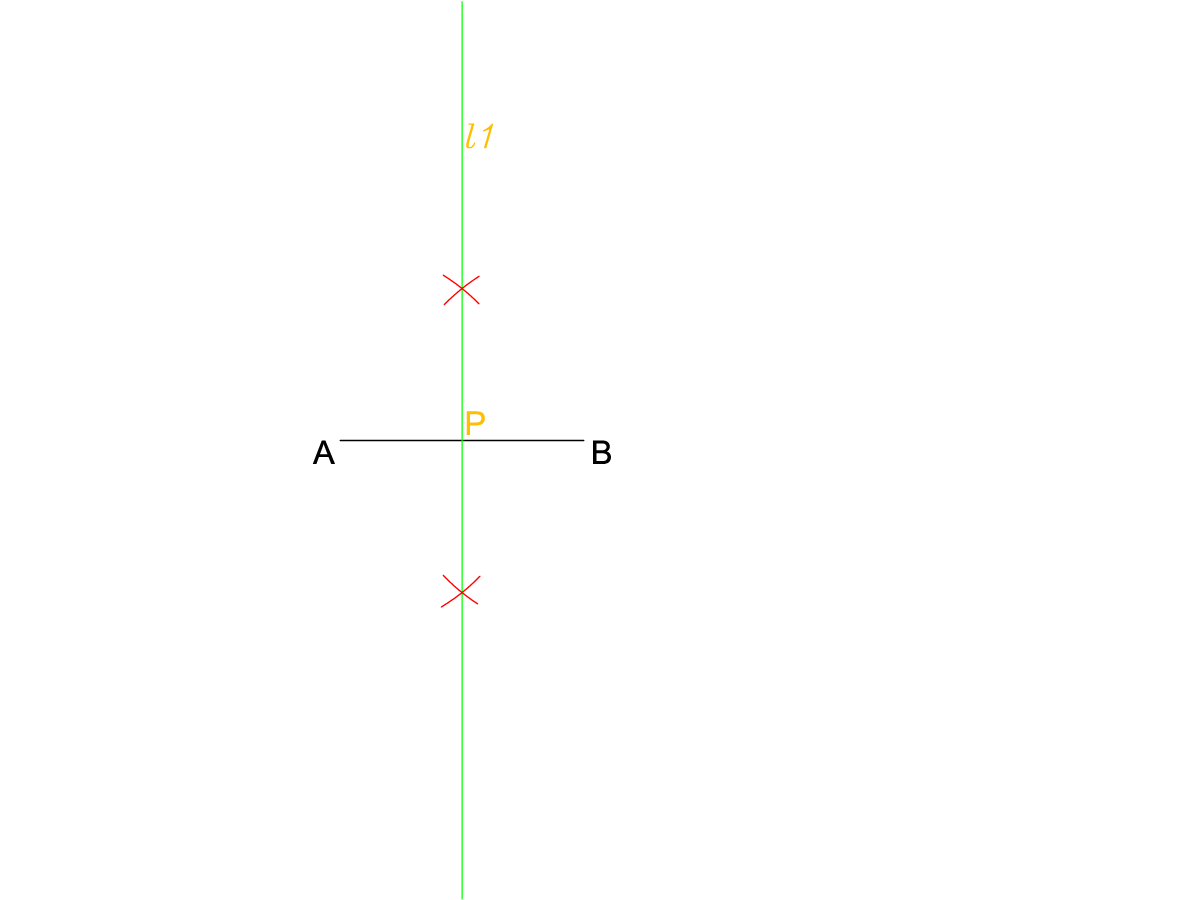
1. 分別以A、B為弧心，以任意 x > |AB| / 2 作弧，連結兩弧交點，得線段AB的垂直平分線l1。l1與AB交於P點。（注：其實只要垂直線即可，不一定要平分）

01

2. 在l1上任取一點Q，分別以任意 y > |PQ| / 2 作弧，連結兩弧交點，得垂直於l1的直線l2。因AB、l2皆垂直於l1，故AB平行於l2。

02

3. 在l2上任取一點A'，以A'為弧心、任意長度a為半徑作弧，使之交l2於點B'。

03

4. 同上，以B'為弧心，a為半徑作弧，使之交l2於點C'。如此類推，作出D'、E'、F'。因|A'B'| = |B'C'| = ... = |E'F'| = a，且A'、B'、...、E'、F'均在同一直線l2上，故B'、C'、...、E'分別為線段A'F'的五等分點，即|A'B'| = |B'C'| = ... = |E'F'| = |A'F'| / 5。

04

5. 作直線AA'、BF'，並使兩者交於M點。

05

 6. 連結MB'，使其交AB於點N。

06

【論證】

• 因角AMB = 角A'MF'，且AB平行於A'F'，故三角形MAB相似於三角形MA'F'，故|AB| / |A'F'| = |MA| / |MA'|。
• 因角AMN = 角A'MB'，且AN平行於A'B'，故三角形MAN相似於三角形MA'B'，故|AN| / |A'B'| = |MA| / |MA'|。
• 綜合上述兩式，得|AN| / |A'B'| = |MA| / |MA'| = |AB| / |A'F'|，
• 移項得|AN| / |AB| = |A'B'| / |A'F'|。
• 根據作圖步驟4，|A'B'| = |A'F'| / 5，
• 故|AN| / |AB| = |A'B'| / |A'F'| = 1/5。
• 即點N為線段AB的五等分點。

【延伸】

要畫AB的n等分點（n為任意正整數）時，均可按上述步驟作圖。只需在作圖步驟4的時候，在l2上畫n+1個等間距的點即可。

【後記】

廢話部分留到最後寫。

筆者原先考慮的是用尺規畫五角星的問題，關鍵步驟是把一個圓五等分，或者是畫一個角的五等分線。結果剛剛畫了個圓，便發現無從入手。直覺認為研究線段的五等分點或會有幫助，於是便開始研究這個問題。

較早前筆者寫個一篇尺規法作三等分點的文章，但那是利用等邊三角形的特殊性質，無法推而廣之到五等分點、七等分點的情況－－換言之，除了摺信紙外，實用意義不大。

後來，筆者在淋浴時（淋浴間是個思考人生的好地方）發現了上述方法的雛型，比三等比點的等邊三角形法還簡單，而且可推廣到n等分點的一般情形。因此，稍作優化後便匆匆發佈－－仿佛發現了新大陸似的。

以上方法還可用來摺信紙，而且只留下三條輔助摺痕，比上次提出的方法還少一條（不過感覺摺的難度大一些，角度挺小的，圖和照片不發了，有興趣讀者自行研究）。

文章第一句便提到三角板，可見它們在筆者心目中的地位（記得筆者那對是從初中一直用到大學的，刻度全磨掉了，30度角還崩掉了，可惜現在不知所蹤了，懷念啊...）。要是可以用三角板，那麼畫平行線便簡單直接得多了，畫n等分點的方法也更簡單。具體過程不詳述了，留一幅圖，讀者可自行參詳：

五角星的問題之後再考慮。

【全文完】