提示:本文既不有趣,亦不有用,純粹因無聊而寫。若 貴讀者有正事在身,敬請繞道。
首先和讀者玩一個很無聊的遊戲:以下是筆者Google到的一些鐘錶廣告,請各位找找其中規律。
您太聰明了!首先您發現了,它們全都是手錶廣告......另外,或許您早就知道了、或許您現在才注意到,所有廣告中的手錶,其時間剛好都在10:10附近!
十點十分早已成為了行業規範,幾乎所有報紙、雜誌、電視、以及其他地方出現的手錶廣告,都會把時間調到那附近(或許廣播電告例外吧,誰關心呢!)。其解釋則眾說紛紜,簡單匯總如下:
- 指針排成V形,V for Victory,有“勝利”之意;
- 時針、分針同時上揚,有美學形式,讓人感到欣悅;
- 指針形狀如同飛鵬展翅,給人奮發之感;
- 指針的角度像微笑;
- 讓時針、分針分居兩側,以襯托錶商的logo;
- 時針、分針、秒針基本把錶面分成三等份,讓顧客看清楚手錶結構;
- 十點十分象徵着十全十美(10 out of 10);
- 經藝術家和心理學家的精心研究,能夠產生最佳的藝術效果;
- 十點十分是一天中最美好的時刻......
不過以上解釋是無法讓筆者滿意的!它們都太籠統、太主觀了。是不是有更“定量”的解釋呢?數學上有一個關於“美”的傳說--黃金分割。筆者想,十點十分是否剛好符合“黃金分割”呢?
黃金分割,簡稱0.618。最完美的身材,肚臍應該落在黃金分割點上,即“腿長”佔總身高的61.8%;畫家和攝影師也常常把“主角”放在“黃金分割”的位置上;據說鸚鵡螺的螺紋與黃金分割有關;它甚至在音樂和經濟學上也有應用......0.618這個數字是這樣來的:
 |
| (詳細推導就不寫了~~) |
於是,趁着上班的發呆時間,筆者開始系統研究起這個問題:在哪些時間,錶盤會被“黃金分割”呢?而十點十分是否其中之一呢?
我們從兩個連小學生都知道的命題出發:
接下來需要一個錶面。如圖,我把“十二點方向”定為“起跑線”,或稱“法線”。這實在無可厚非,每天伊始,時針、分針、秒針都是從這裡“起跑”的。另外我還規定,時針與“法線”的夾角記為α,分針的角度則為β。
現在來考慮,在 H 時 M 分的時候,時針和分針會處在甚麼角度呢?(秒的影響恕不考慮,理由將在下面闡述)分針的情況較簡單,因為每分鐘= 6o,M 分鐘就等於 M × 6o,即:
時針的情況複雜一些。首先一小時包含5小格,即5 × 6o = 30o,因此 H 小時就等於 H × 30o,然後分鐘 M 對它也是有影響的:每60分鐘,時針移動5小格,即 5 × 6o = 30o ,因此每分鐘移動 30o ÷ 60 = 0.5o,M 分鐘就移動了 M × 0.5o。綜合兩個因素,時針的角度α為:
我們從兩個連小學生都知道的命題出發:
- 一圈有360度;
- 一小時有60分鐘。
接下來需要一個錶面。如圖,我把“十二點方向”定為“起跑線”,或稱“法線”。這實在無可厚非,每天伊始,時針、分針、秒針都是從這裡“起跑”的。另外我還規定,時針與“法線”的夾角記為α,分針的角度則為β。
現在來考慮,在 H 時 M 分的時候,時針和分針會處在甚麼角度呢?(秒的影響恕不考慮,理由將在下面闡述)分針的情況較簡單,因為每分鐘= 6o,M 分鐘就等於 M × 6o,即:
時針的情況複雜一些。首先一小時包含5小格,即5 × 6o = 30o,因此 H 小時就等於 H × 30o,然後分鐘 M 對它也是有影響的:每60分鐘,時針移動5小格,即 5 × 6o = 30o ,因此每分鐘移動 30o ÷ 60 = 0.5o,M 分鐘就移動了 M × 0.5o。綜合兩個因素,時針的角度α為:
好,現在來看看時針、分針之間的夾角:
- 如果時針走在分針前面,正如上圖那樣、或者十點十分的情況,那麼其夾角應為 (α-β);
- 如果情況相反,分針走在前面,例如在一點五十分的時候,其夾角應該反過來,為 (β-α)。
回到“黃金分割”的問題上。我們已經知道,黃金分割率的值為0.618,換言之,只要時針、分針的夾角為360o × 0.618 = 222.48o,或者為360o × (1 - 0.618) = 137.52o的時候,錶面被黃金分割了。列成數學式則為:
合併同類項、化簡,得到“黃金分割”的條件如下:
至此我們仍未得到一些明確的數字,亦不知道十點十分是否滿足黃金分割,不過已經呼之欲出了。很明顯,小時 H 只能取0~11(或者1~12,結果是一樣的)的整數,我們還沒有見過“7.36時13分”這樣不倫不類的表達法。同樣,分鐘 M 也應該是0~59的數,至於能不能是小數,筆者認為是可以的(雖然“9時23.47分”的表達法同樣荒誕不經),這裡沒有嚴謹的理論支持,而僅僅是筆者的直覺。讀者如有高見,敬請不吝賜教!
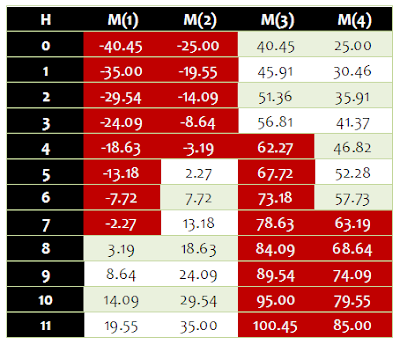
我把上述4個“黃金分割”條件、以及“H 只能取0~11的整數”統統輸入到強大的Excel中,並篩走其中不合理的 M 值,得到這樣一張表:
此表列出了所有“黃金分割”的時間,其中紅底為“不合理”、應該篩去的時間。由表中可見,這些時間包括了00:40、00:25、01:46、01:30......有趣的是,所謂的“不合理”只是不符合習慣而已,例如“01:-35.00”表示“差35分鐘到1點”,相當於00:25.00;“01:-19.55”等同於“00:40.45”;而“06:73.18”則是“07:13.18”的另一種表述而已......
至此“秒“依然被筆者無情地忽略。其原因有三:
- “秒”對分針角度的影響畢竟較小(對時針更是微不足道了),不像“分鐘”對時針的影響那麼明顯;
- 更重要的是,一旦把“秒”也考慮進來,上述的Excel表會變得很大、很複雜,可能還要做成三維表了;
- 最後,“黃金分割率”跟圓周率π一樣,是個無理數,0.618只是近似值。對於不講道理的人,我們何必太較真?!
為了更加直觀,筆者把上述表格製成一幅幅錶面圖,讓讀者欣賞一下錶盤上的各種黃金分割:
很遺憾十點十分並不在其中,比較接近的是十點十四分。偏偏,錶商和廣告商一般更喜歡偏向10:08的位置,而不是10:14處。看來筆者的“定量解釋”和“黃金分割”注定失敗了......
好在數學上還有另一個美麗的傳說--對稱。十點零八分,不就是以“法線”為軸的對稱嗎?
實驗雖然失敗了,工作卻不是毫無意義的:當讀者上班、上學太無聊時,不妨取出手錶,守候一個個黃金分割的“checkpoint”、欣賞一次次完美的分割比例,這樣,或許漫長無聊的時間會更 充實 好過一些。















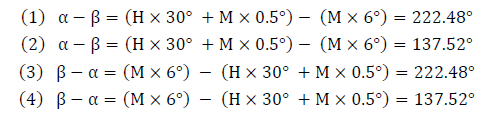

.jpg)
沒有留言:
張貼留言