六X彩中獎概率

最近認真研究起“六X彩中獎概率”這個問題，並且把頭獎至安慰獎的概率都列出來了...

I've been deeply thinking about the probability of winning a 'm**k-six' lottery for days, and have already figured out the expressions for each division prize.

結果一算，不對了，中頭獎的概率比中二獎還大......
The result is, however, depressing. It gives the conclusion that 'it's easier to win the 1st division prize  than the 2nd prize.'

肯定是哪裡搞錯了，要再檢查一下......
There must be something wrong, better check it again......

.........已解決。
.........Problem solved.

※※※※※※※※※※※※※※※※※※

六X彩中獎概率是個非常有意思、有實用性的概率論問題，可惜由於某些原因，沒有老師敢在課堂上佈置這道題目。筆者亦因此從不把它當回事。

六X彩的規則大家都相當熟悉了：投注者從1~49號中任意選出6個號碼，組成“一注”；莊家則從這49個號碼中“隨機”抽出6個中獎號碼，以及1個特別號碼：

• 如果投注者所選的6個號碼與6個中獎號碼一致（”中6個字”），便獲得頭獎；
  中任意5個中獎號碼及1個特別號碼（“中5.5個字”），便獲得二獎；
• 投注者所選的6個號碼中，若其中5個為中獎號碼（"中5個字"），則獲得三獎；
• ......（依此類推）；
• 最後，若投注者”中3個字”，便會獲得安慰獎；

從數學的角度，不論中的是甚麼獎，其概率都可以用一個分數X/Y來表示，其中分母Y是可能出現的一切攪珠結果的數目，分子X是能夠讓你中獎的攪珠結果的數目。以下逐一說明：

(0) 分母：

　　 六X彩總共有多少攪珠結果呢？第一步要從49個號碼中任意選出6個中獎號碼，即有[49C6]（組合函數，其值可以用Excel計算：輸入公式"=COMBIN(49,6)"即可，下同）種可能；第二步要從剩下的49-6=43個號碼中選一個特別號碼，即[(49-6)C1]。

　　二者相乘，即一共有[49C6]*[(49-6)C1]種可能的攪珠結果。這就是以下各種概率的分母了。

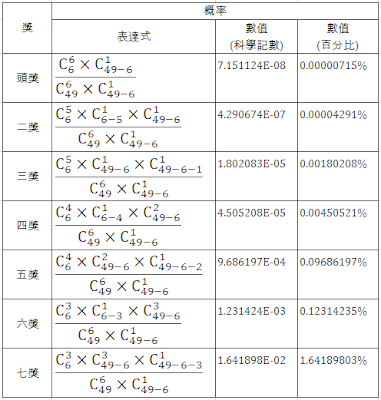
(1) 頭獎：

　　假設您買了一注六X彩，我們已經知道，它一共有[49C6]*[(49-6)C1]種可能的攪珠結果，那麼，有多少種攪珠結果能讓您中頭獎、一夜致富呢？

　　許多人的第一反應是：“有且只有一種：必須6個數字全中！”其實當中並不只一種。假設您買的是1,2,3,4,5,6，而攪出的6個中獎號碼亦正是1,2,3,4,5,6，那麼，不管特別號碼是7、8、還是47，您都能夠獲得頭獎獎金。換言之，中獎號碼相同、特別號碼不同，數學上亦被視為不同的攪珠結果。

　　因此，能夠讓您中頭獎的攪珠結果一共有[6C6]*[(49-6)C1]種：[6C6]是指6個中獎號碼都必須跟您所選定的號碼一致，而[(49-6)C1]則表示最後1個特別號碼可從剩下的(49-6)個號碼中任選，不管選甚麼您都能中頭獎。

　　即中六X彩頭獎的概率為：

 

(2) 二奬：

　　類似地，我們先分析有多少種攪珠結果可讓您中二奬。

　　首先，其中5個中奬號碼必須出自您所選定的6個號碼中，即[6C5]；然後，您的”一注”裡剩下的那個號碼必須為特別號碼，即[(6-5)C1]；最後還剩了1個中獎號碼，可以是其餘(49-6)個號碼中的任意一個，即[(49-6)C1]。

　　因此，一共有[6C5]*[(6-5)C1]*[(49-6)C1]種攪珠結果能夠讓您中二奬；而中二獎的概率可用下式表示：

(3) 三奬：

同上，其中5個中獎號碼必須出自您的”一注”中，即[6C5]；而最後一個中獎號碼則必須來自您的6個心水號碼以外（否則便是”中頭獎”的情況了），即[(49-6)C1]；最後，特別號碼既不能是6個心水號碼中的一個（否則便是”中二奬”），亦不可能等於最後一個中獎號碼，因此只剩下49-6-1種選擇了，即[(49-6-1)C1]。

　　即可以中三獎的攪珠結果共有[6C5]*[(49-6)C1]*[(49-6-1)C1]種，而中三獎的概率為：

(4) 四奬：

　　很囉嗦地把四奬的情況也寫出來，只為把問題解說得清清楚楚。首先，其中4個中獎號碼必須出自6個心水號碼中，即[6C4]；接下來，特別號碼可以是另外6-4=2個心水號碼中的任意一個，即[(6-4)C1]；最後，餘下的2個中獎號碼與6個心水號碼則是”河水不犯井水”，即它們只能從剩下的49-6個號碼中挑選，即[(49-6)C2]。

　　因此，結果一共有[6C4]*[(6-4)C1]*[(49-6)C2]個。而四獎概率則為：

(5) ~ (7) 五至七奬：

　　五至七獎的情況，基本上也是按上面的思路，即把攪珠結果分成三部份，分別考慮，然後相乘起來即可：相符的中獎號碼、不相符的中獎號碼、特別號碼。

　　五至七獎的概率分別如下式所列：

 （圖）

經計算，各級獎項的中奬概率如下表所示：

※※※※※※※※※※※※※※※※※※

有了上表的數據，我們可以估算六X彩這項“投資產品”的期望回報了。

然而，由於頭、二、三獎的派彩獎金不是固定值，而是隨彩池金額、中獎人數而異的，因此以下計算並無代表性。

以下以2012年1月31日的結果為例計算，因為該次的頭獎金額是有史以來最高的。該次金多寶的派彩結果如下：

假設攪珠公平公正無“造馬”，亦不考慮打稅的問題，則獎金的期望值=各級獎金的概率*各級獎金金額再加在一起。其結果為：

 

即每注的期望獎金是10.40元。以現時每注10元投注額計算，回報率為4.0%。期望回報率比二年人民幣定期還高，更是遠超港元／澳門元定期，難怪學校不敢讓學生算了（當然，只有超級金多寶而且一注獨中頭獎時才是4.0%的期望回報率，正常情況下仍是負回報的）......

雖說中獎機率只有不到2%，而有98%以上機會虧錢，可是六X彩要買了才會中，據說這是道理來的......