註:本文僅供筆者自娛自樂之用,內容相信沒有人會看的,有興趣的讀者直接看結論即可,多謝合作!
相信大家都聽說過“賭仔磨爛蓆”這句俗語,大概就是“長賭必輸”的意思。人們說這句說話時,更多是從心理角度出發的;可是從數學上分析,也的確有其道理。賭博遊戲縱然五花八門,卻有一個重要的共通點:贏錢總比輸錢難。換言之,“產出”的期望值總比“投入”低。
舉個人盡皆知的例子--“賭大小”:三顆骰子點數相加,10點或以下算“開大”、11點或以上算“開小”,押對了則1賠1,押錯則全賠。“開大”、“開小”的概率是一樣的,但概率略小於50%,因為還有“圍骰通殺”的情況。“圍骰”的概率看上去很小,然而,計算結果發現,正是由於這個微不足道的“不公平”不斷累積疊加,導致了“賭仔磨爛蓆”的情況。
以下就以“賭大小”為例,分析一下“賭仔磨爛蓆”是如何發生的。以下討論默認賭場、莊家沒有“出千”,擲骰子時每一面的概率相同,均為1/6。
首先論證一下“開大”跟“開小”的概率為甚麼是一樣的。當然也可以用正常的“排列組合”來分析,但筆者想了個“旁門左道”,似乎更直觀一些。以下就以“賭大小”為例,分析一下“賭仔磨爛蓆”是如何發生的。以下討論默認賭場、莊家沒有“出千”,擲骰子時每一面的概率相同,均為1/6。
※※※※※※※※※※※※※※※※※※
記集合{1,2,3,4,5,6}為X,可知對任意的x屬於X,有且僅有另一個x'屬於X,使得x+x'=7(聽上去玄裡玄乎的,但如果改寫成 y=7-x 或 f(x)=7-x 就十分清晰了。),而且x不等於x'。在這個案例中,筆者姑且把x和x'稱為一對“共軛數”。
顯然,以上就是對於一顆骰子的情況,即對於任意的擲骰結果x,都有且僅有一個共軛x',使得x+x'=7。現在假設有三顆骰子A、B、C,其擲骰結果分別為a、b、c,而其共軛數分別記為a'、b'、c'。
大家知道,根據賭博規則,當三粒骰子之和小於或等於10時算“開小”,大於或等於11算“開大”(圍骰除外,稍後便會討論)。假設a+b+c<=10,則其共軛數:
a'+b'+c'=(7-a)+(7-b)+(7-c) =21-(a+b+c)
>=21-10=11
換言之,對任何一個“開小”的擲骰結果,都有一個共軛的“開大”結果與之一一對應;反之亦然。因此,有多少個“開小”的組合,就有多少個“開大”的組合,故兩者概率相等。
接着討論“圍骰通殺”的情況。一顆骰子有六面,有6個可能的擲骰結果,三顆骰子就可能有6x6x6=216(嚴格而言是C(6,1) x C(6,1) x C(6,1))種結果,根據上面的討論,“開大”、“開小”的組合一樣多,均為216/2=108種。
然而,當三顆骰子結果相同時,即擲出[1,1,1]、[2,2,2]、......、[6,6,6]六種(嚴格而言是C(6,1) x C(1,1) x C(1,1))結果時被稱為“圍骰”,此時不管“押小”還是“押大”都要輸錢,無論加出來的結果是小於10還是大於11。因此,“開大”的組合中要扣除[4,4,4]、[5,5,5]、[6,6,6]三種,剩108-3=105種,實際“開大”的概率則為105/216=48.6111%,同理,實際“開小”的概率也是48.6111%。(顯然,[1,1,1]與[6,6,6]、[2,2,2]與[5,5,5]、[3,3,3]與[4,4,4]也互成共軛對)
換言之,當閣下在賭場下注押大(或押小)時,有48.6111%機率贏錢(以下記為“p”),有100%-48.6111%=51.3888%輸錢(以下記為“1-p”)。
假設“賭仔”有本金$10,000.00(以下記為A),那麼他一注“曬冷”、或者平均分成100注慢慢“磨”,勝算分別幾何?接下來便將分情況討論。
【1. 一注“曬冷”】
一注“曬冷”的情況,其實上面已經討論過了。一個回合,只有“輸”或“贏”兩種可能,其中贏錢的概率就是p,即48.6111%;輸錢的概率是1-p,即51.3888%。
投入$10,000,有48.6111%機會“產出”$20,000,有51.3888%“產出”$0(全賠),因此“產出”的期望值為:
分成兩回合,情況複雜一些。每回合各有“輸”、“贏”兩種結果,因此結果共有2x2=4種(嚴格而言是C(2,1) x C(2,1)種),分別是“兩戰全勝”、“先勝後負”、“先負後勝”、“兩戰皆北”。其中只有前者能贏錢、只有後者會輸錢、中間兩者則能“全身而退”。因此,勝、和、負的概率分別為:
【3. 分成三注】
分成三回合,情況就更複雜了。每回合有“輸”“贏”兩種結果,故一共有2x2x2=8種情況(C(2,1) x C(2,1) x C(2,1)),其中:
這次的結論就比較豐富了:
經過本例的分析,“一般情況”也呼之欲出了。
【4. n為奇數的一般情況】
直接寫結果吧!假設“賭仔”將本金A平均分成n份(n為奇數),分n回合下注,則他勝出其中 i 回合的概率為:
※※※※※※※※※※※※※※※※※※
然而,當三顆骰子結果相同時,即擲出[1,1,1]、[2,2,2]、......、[6,6,6]六種(嚴格而言是C(6,1) x C(1,1) x C(1,1))結果時被稱為“圍骰”,此時不管“押小”還是“押大”都要輸錢,無論加出來的結果是小於10還是大於11。因此,“開大”的組合中要扣除[4,4,4]、[5,5,5]、[6,6,6]三種,剩108-3=105種,實際“開大”的概率則為105/216=48.6111%,同理,實際“開小”的概率也是48.6111%。(顯然,[1,1,1]與[6,6,6]、[2,2,2]與[5,5,5]、[3,3,3]與[4,4,4]也互成共軛對)
換言之,當閣下在賭場下注押大(或押小)時,有48.6111%機率贏錢(以下記為“p”),有100%-48.6111%=51.3888%輸錢(以下記為“1-p”)。
※※※※※※※※※※※※※※※※※※
假設“賭仔”有本金$10,000.00(以下記為A),那麼他一注“曬冷”、或者平均分成100注慢慢“磨”,勝算分別幾何?接下來便將分情況討論。
【1. 一注“曬冷”】
一注“曬冷”的情況,其實上面已經討論過了。一個回合,只有“輸”或“贏”兩種可能,其中贏錢的概率就是p,即48.6111%;輸錢的概率是1-p,即51.3888%。
投入$10,000,有48.6111%機會“產出”$20,000,有51.3888%“產出”$0(全賠),因此“產出”的期望值為:
Exp = 48.6111% x $20000 + 51.3888% x $0 = $9722.22【2. 分成兩注】
分成兩回合,情況複雜一些。每回合各有“輸”、“贏”兩種結果,因此結果共有2x2=4種(嚴格而言是C(2,1) x C(2,1)種),分別是“兩戰全勝”、“先勝後負”、“先負後勝”、“兩戰皆北”。其中只有前者能贏錢、只有後者會輸錢、中間兩者則能“全身而退”。因此,勝、和、負的概率分別為:
勝(W):P(W) = p x p = 48.6111% x 48.6111% = 23.6304%由於分成了兩注,每一回合投入A/2=$5,000,押對則產出2x(A/2)=$10,000,押錯則產出$0。因此,“兩戰全勝”總產出為$10,000+$10,000=$20,000,“一勝一負”產出為$10,000+$0=$10,000 ,“兩戰皆北”的產出則為$0。因此期望值為:
和(D):P(D) = p x (1-p) + (1-p) x p = 24.9807% + 24.9807% = 49.9614%
負(L):P(L) = (1-p) x (1-p) = 51.3888% x 51.3888% = 26.4082%
Exp = P(W) x $20000 + P(D) x $10000 + P(L) x $0 = $9722.22由此可得出兩個比較重要的發現:
- 偶數的情況與奇數不同。分成偶數注時,結果可以“打和”,而奇數必定分出勝負;
- 分成兩注時,“贏錢”的概率雖與“一注曬冷”的情況不同,但期望值仍相同。
【3. 分成三注】
分成三回合,情況就更複雜了。每回合有“輸”“贏”兩種結果,故一共有2x2x2=8種情況(C(2,1) x C(2,1) x C(2,1)),其中:
- 三連勝的情況只有C(3,3)=1種,概率P(3) = C(3,3) x p x p x p = C(3,3) x p^3
- 兩勝一負有C(3,2)=3種(即[勝勝負]、[勝負勝]、[負勝勝]),概率P(2) = C(3,2) x p x p x (1-p) = C(3,2) x p^2 x (1-p)
- 一勝兩負則有C(3,1)=3種,概率P(1) = C(3,1) x p x (1-p) x (1-p) = C(3,1) x p x (1-p)^2
- 三戰盡墨的有C(3,0)=1種,概率P(0) = C(3,0) x (1-p) x (1-p) x (1-p) = C(3,0) x (1-p)^3
勝(W):P(W) = P(3) + P(2) = 11.4870% + 36.4302% = 47.9172%期望值分析:對每一回合,投入均為A/3=$3,333.33(先不管實際操作是否可行),押對則產出2 x (A/3) = $6,666.67,押錯則產出$0。因此:
負(L) :P(L) = P(1) + P(0) = 38.5119% + 13.5709% = 52.0828%
押對三次的產出E(3) = 2 x (A/3) x 3;因此,總產出的期望值為:
押對兩次的產出E(2) = 2 x (A/3) x 2 + 0 x 1;
押對一次的產出E(1) = 2 x (A/3) x 1 + 0 x 2;
全部押錯的產出E(0) = 2 x (A/3) x 0 + 0 x 3。
Exp = P(3) x E(3) + P(2) x E(2) + P(1) x E(1) + P(0) x E(0)代入相關數據,得Exp=$9,722.22。
這次的結論就比較豐富了:
- 分成奇數回合後,當“勝”的回合多於總回合數的一半時就能贏錢。例如本例中,總回合數為3,一半即3/2=1.5,因此“三連勝”(3>1.5)或“兩勝一負”(2>1.5)都屬於“贏錢”,而“一勝兩負”(1<1.5)及“三戰盡墨”(0<1.5)均屬“輸錢”;
- 分成三注後,贏錢的概率為47.9172%,略低於“一注曬冷”的48.6111%;
- 期望值仍跟之前一樣,為$9,722.22。
經過本例的分析,“一般情況”也呼之欲出了。
【4. n為奇數的一般情況】
直接寫結果吧!假設“賭仔”將本金A平均分成n份(n為奇數),分n回合下注,則他勝出其中 i 回合的概率為:
當i>(n/2),即i>=[(n+1)/2]時,“賭仔”贏錢,因此贏錢的概率為:
當i<(n/2),即i<=[(n-1)/2]時,“賭仔”輸錢,即輸錢概率為:
而“賭仔”將本金A分成n份,每回合投入A/n,若獲勝則產出2 x A/n,失敗則產出0。因此,假設“賭仔”獲勝 i 回合,則他收獲的“產出”為:E(i) = 2 x A/n x i + 0 x (n-i)
故總期望值為:
【5. n為偶數的一般情況】
n為偶數時,形式上也跟奇數差不多,當i>(n/2)時,“賭仔”還是贏錢的, 當i<(n/2)時,“賭仔”還是輸錢的。不同之處在於,因為n是偶數,所有n/2是整數,因此i可以等於n/2,此時結果為“打和”。
從n回合中勝出i回合的概率仍為:
當i>(n/2),即i>=[(n/2)+1]時[此處與奇數情況稍有差異],“賭仔”贏錢,因此贏錢的概率為:
當i<(n/2),即i<=[(n/2)-1]時,“賭仔”輸錢,即輸錢概率為:
當i=n/2時則打和,其概率為:
總期望值為:
【6. 當n很大很大】
以上第3點的最後部分,筆者就曾用Excel表格計算n=3、5、7的情況。然而,當n很大很大時,用表格的方格無疑比較麻煩,例如當n=1000時,就要列一個1000列的表格。為簡便操作,筆者寫了個巨集如下:
直接輸入變量n,再運行巨集(Alt + F8),便可迅速計得“賭仔”的勝算。以下列舉一些數據:
奇數情況:
偶數情況:
通過以上數據及圖表,相信各位已經感受到“賭仔磨爛蓆”的道理了。
【7. 假如沒有圍骰通殺】
上面已經討論過,不考慮“圍骰通殺”的時候,開大、開小的概率相同,均為50%,即p=(1-p)=50%。若把檔案中的p和(1-p)都設為50%再執行巨集,那麼可以發現,即使“賭仔”與莊家激戰999回合,依然難分高下。
所以,正如文章開頭所說的,正是由於微不足道的“不公平”不斷累積疊加,才導致了“賭仔磨爛蓆”的情況。
【8. 思考題】
以上已經列出了一般情況的計算公式了,可是公式形式比較複雜,特別是n比較大的時候,必須用電腦才能計算。因此,能否通過泰勒多項式等方法來簡化公式呢?只怪筆者當年微積分沒學好,曲線圖上也無法擬合出一條很準確的曲線,這個問題只好留待各位高人賜教。
從n回合中勝出i回合的概率仍為:
當i>(n/2),即i>=[(n/2)+1]時[此處與奇數情況稍有差異],“賭仔”贏錢,因此贏錢的概率為:
當i<(n/2),即i<=[(n/2)-1]時,“賭仔”輸錢,即輸錢概率為:
當i=n/2時則打和,其概率為:
總期望值為:
【6. 當n很大很大】
以上第3點的最後部分,筆者就曾用Excel表格計算n=3、5、7的情況。然而,當n很大很大時,用表格的方格無疑比較麻煩,例如當n=1000時,就要列一個1000列的表格。為簡便操作,筆者寫了個巨集如下:
直接輸入變量n,再運行巨集(Alt + F8),便可迅速計得“賭仔”的勝算。以下列舉一些數據:
奇數情況:
- 一注“曬冷”,勝算為48.6111%;
- 分成9注,勝算為46.5855%;
- 分成99注,勝算為39.0837%,不足四成;
- 分成999注,勝算為18.9874%,不足兩成;
- 分成9999注,電腦計不出來了......
偶數情況:
- 分成2注,有23.6304%機會贏錢,另有49.9614%機會全身而退;
- 分成10注,勝算為34.3282%,另有24.5146%機會全身而退。看似勝算高了,其實輸錢的概率也大幅從26.4082%升至41.1572%;
- 分成100注,勝算為35.2549%,而打和機會為7.6576%,輸錢機會為57.0875%;
- 分成1000注,勝率僅餘18.1300%,另有1.7148%機會打和,失敗率逾80%......
 |
| 奇數情況 |
 |
| 偶數情況 |
通過以上數據及圖表,相信各位已經感受到“賭仔磨爛蓆”的道理了。
【7. 假如沒有圍骰通殺】
上面已經討論過,不考慮“圍骰通殺”的時候,開大、開小的概率相同,均為50%,即p=(1-p)=50%。若把檔案中的p和(1-p)都設為50%再執行巨集,那麼可以發現,即使“賭仔”與莊家激戰999回合,依然難分高下。
所以,正如文章開頭所說的,正是由於微不足道的“不公平”不斷累積疊加,才導致了“賭仔磨爛蓆”的情況。
【8. 思考題】
以上已經列出了一般情況的計算公式了,可是公式形式比較複雜,特別是n比較大的時候,必須用電腦才能計算。因此,能否通過泰勒多項式等方法來簡化公式呢?只怪筆者當年微積分沒學好,曲線圖上也無法擬合出一條很準確的曲線,這個問題只好留待各位高人賜教。
※※※※※※※※※※※※※※※※※※
“賭仔磨爛蓆”,據說泡妞也是這樣。


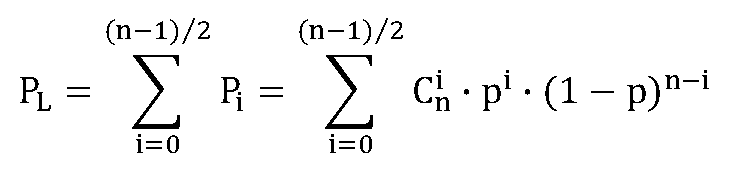








沒有留言:
張貼留言